Modulo Y Argumento De Un Numero Complejo Modulo

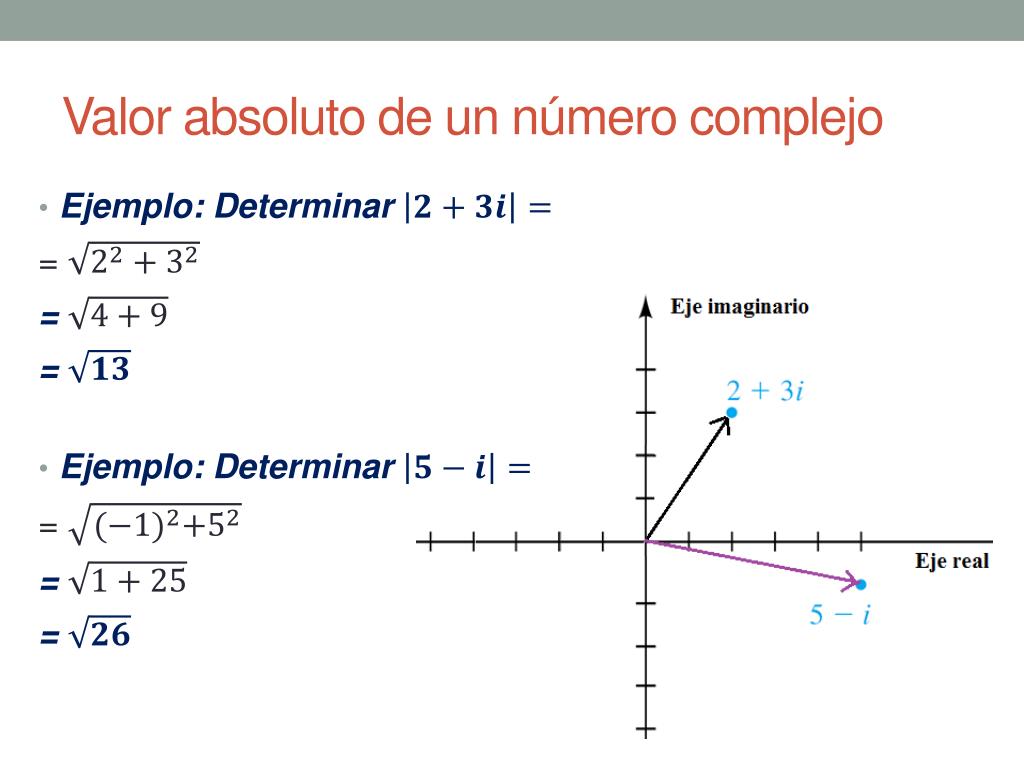
Modulo O Valor Absoluto De Un Numero Complejo Ejemplos Nuevo Ejemplo

Una vez vistos cómo son, vamos a ponerlos en contexto con el resto de conjuntos numéricos: Los números enteros hacen referencia a los números naturales, es decir, todos aquellos números que no contienen parte decimal: 3, -1, 10.; Los números racionales son el cociente de dos números naturales: 3/10, 7/9.; Los números irracionales son aquellos que no pueden ser expresados como una.

Módulo de un número complejo. YouTube

Números complejos. Componentes reales e imaginarios, ángulos de fase. En MATLAB ®, i y j representan la unidad imaginaria básica. Puede utilizarlos para crear números complejos como 2i+5. También puede determinar las partes reales e imaginarias de los números complejos y calcular otros valores comunes, como la fase y el ángulo.

Módulo y Argumento de un número complejo YouTube

Comprueba tu comprensión de Números complejos con estas NaN preguntas. Inicia la prueba. Este tema cubre: - Sumar, restar, multiplicar y dividir números complejos - Plano complejo - Valor absoluto y ángulo de números complejos - Coordenadas polares de números complejos.

Algebra lineal u1

Para calcular su módulo, seguimos los siguientes pasos: 1. **Elevamos al cuadrado** tanto la parte real como la parte imaginaria del número complejo. 2. **Sumamos los resultados** obtenidos en el paso anterior. 3. **Calculamos la raíz cuadrada** de la suma obtenida en el paso anterior.

¿Qué son los números complejos? YouTube

Argumento de un número complejo. La calculadora permite calcular online el argumento de un número complejo. El plano está provisto de una referencia ortonormal directa (O, i , j ) ( O, i →, j →). Deje z un número complejo distinto de cero y M su imagen. Llamamos al argumento de z, cualquier medida, expresada en radianes, del ángulo (i.

Magnitud de un número complejo YouTube

El módulo de un número complejo z=a+ib (donde a y b son reales) es el número real positivo, anotado |z| , definido por : |z| = a2 + b2− −−−−−√ | z | = a 2 + b 2. La calculadora de módulo permite calcular el módulo de un número complejo online . Para el cálculo del módulo de un complejo, es suficiente ingresar el número.

Álgebra Modulo y argumento de un numero complejo. Álgebra

Forma binómica. Un número complejo Z (no confundirse con C, que es el conjunto al que pertenecen) se puede representar de la forma: Perteneciendo a y b al conjunto de los números reales. Esta forma de escribir los números complejos corresponde a la forma binómica, que tiene dos partes: a = Parte real. b = Parte imaginaria.

29. Módulo o valor absoluto de un número complejo YouTube

Las coordenadas polares dan una alternativa a la representación de números complejos. En las coordenadas polares, un número complejo z se define por los módulos r y el ángulo de fase phi.El módulo r es la distancia desde z hasta el origen, mientras que la fase phi es el ángulo que va en contra de las agujas del reloj, medido en radianes, desde el eje positivo de las X hasta el segmento.

Números Complejos (parte II)

Valor absoluto. El valor absoluto (o módulo) de un número real es el valor no negativo correspondiente que prescinde del signo. Para un valor real a, el valor absoluto es: a, si a es mayor o igual que cero. -a, si a es menor que cero. abs(-0) devuelve 0.

Módulo de un número complejo YouTube

Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra , o en forma polar ).

Módulo, Gráfica y argumento de un número complejo Vídeo 1 YouTube

Partiendo de la señal exponencial mencionada en este glosario, podemos definir la señal exponencial compleja cuando la base "a" es un valor complejo: Mediante el código Matlab siguiente, tratamos y representamos una exponencial compleja de ejemplo. Se solicita al usuario el valor de módulo y fase de "a", y se representa la parte.

NUMEROS COMPLEJOS 02 MODULO ARGUMENTO EJEMPLOS YouTube

Unidad 4. Números Complejos El módulo de un número complejo 3.Si z= a+ib, entonces p a 2+ b2 a p a2 + b2 puesto que b 0. La otra se prueba de manera análoga 4.Si z= a+ ib, entonces z= a ib, y claramente tenemos que jzj=

Modulo Y Argumento Modulo

1. Módulo y argumento. Dado un número complejo en su forma binómica z = a + bi z = a + b i, Se define el módulo de z z como. Se define el argumento de z z como. Nota 1: la función arcotangente proporciona el ángulo entre -45º y 45º. Nota 2: observad que, por ejemplo, la función arcotangente proporciona el mismo ángulo para z = a −.

Modulo Y Fase De Un Numero Complejo Modulo

Los números complejos son el conjunto de los pares de valores (a ,b) representados en el plano complejo: C={(a ,b)/a∈R ,b∈R} . También podemos expresar C como un producto cartesiano: C={(a,b)∈R x R} . El primer elemento del par de valores (a ,b) se denomina parte real. Y el segundo es la parte imaginaria.

Modulo Y Fase De Un Numero Complejo Modulo

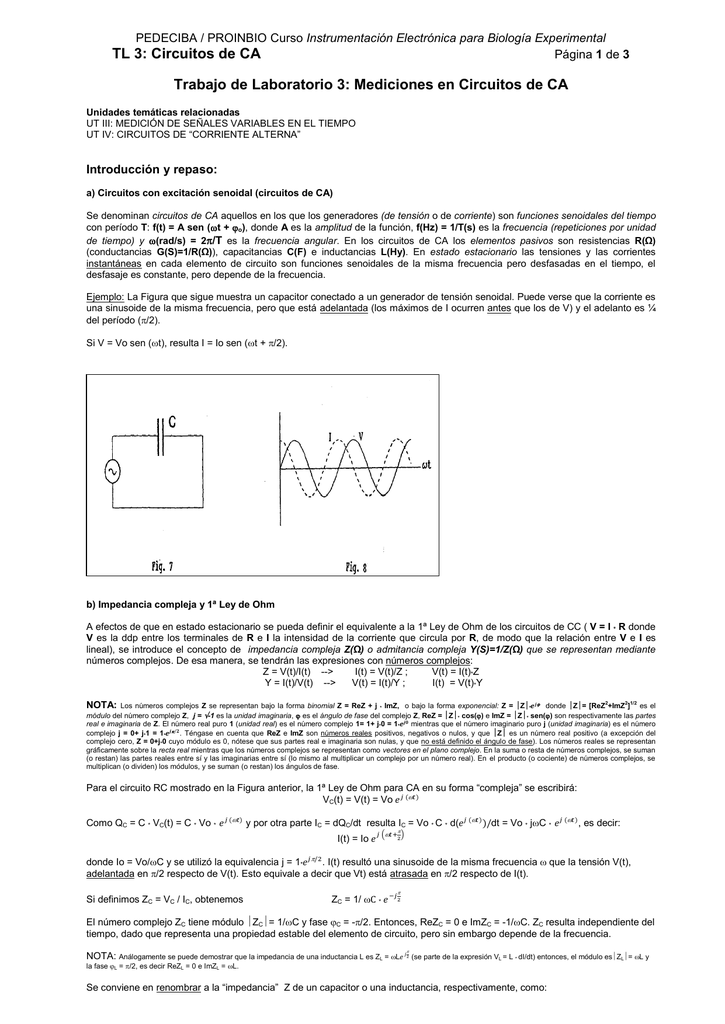
Dos ejemplos de cómo hallar el módulo y la fase de un cociente y un producto de números complejos.

Modulo Y Argumento De Un Numero Complejo Modulo

En el plano complejo, si z es el afijo del punto M, entonces el módulo de z corresponde a la distancia del punto M al origen. En matemáticas, el módulo de un número complejo es el número real positivo que mide su tamaño y generaliza el valor absoluto de un número real.Esta noción es particularmente útil para definir una distancia en el plano complejo.